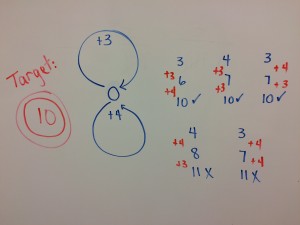Backstory to this post:
Teaching in an inquiry-based school, we don’t isolate “subjects” as most traditional schools do. The beauty of this model is that kids really get to make connections. Science doesn’t just happen at a certain time of day, and it usually involves many other content areas as well. I love when my students are able to connect on their own that music is science is math is history is communication… and so on.
Although we don’t teach subjects in isolation all day, we do spend some time looking at content areas on their own for supporting understanding.
Math is a great example of one “subject” in our school that receives some supplemental time. It still looks different, though, because we meet each child where he/she is and help to move more deeply into understanding.
(I started to type “move forward,” but that’s not necessarily what happens, nor should it.)
The FOCUS of this post:
The problem with math in so many traditional schools is that there is a push to move kids along, rather than guide them into understanding. If you memorize facts easily, you’re going to do well in math early on. The problem with how math is often taught – and how most people think it should be taught – is that we focus so much on the “abstract” — the written facts. My friend Rafranz Davis says, “experiencing math starts with the ‘why,’ not the ‘how.'” I love this! Multiplication tables and formulas, for example, are the how, not the why.
Because so many of us, educators and non-educators alike, were taught with a focus on the math facts, we tend to forget that the conceptual understanding — the “concrete” and “representational” aspects of numbers — is entirely more important than what we memorize. A lot of students who do well in elementary or primary math classes find themselves struggling in pre-algebra or other math classes that require an understanding of what those facts mean, how numbers are related, the underlying patterns in those facts, and how it all connects. <— The WHY
Flash cards, worksheets, and apps that only focus on drilling facts are not what our kids need. They do not show us what our children have learned and understand about math.
BUT… this is where so much time, effort, and concerns lie. If students do not have their multiplication tables memorized by 3rd or 4th grade, they’re labeled as behind their peers. As a teacher, this frustrates me immeasurably. Yes, we want kids to be fluent in their facts, but the problem is when we assign a date and time to when they must have these facts memorized.
You might have a child who memorizes easily, but doesn’t truly understand what the fact means. I once had a student who knew that 5×3=15, but did not know that 5 groups of 3 items was the meaning behind it. Another one of my students understood that multiplication was grouping, but she could not recall fluently each fact if put on the spot.
Teaching a K/1 class for the first time has reinforced my philosophy of how I teach math- they WHY comes before the HOW. An example from today sealed the deal:
I have four students, all boys, in my class. (I know. Yes, I typed “four.”)
Every one of these boys, ages 5 and 6, is in a different place in his understanding of addition and subtraction facts. Some can skip count by 7s. Some are still struggling with addition and subtraction facts up to 10.
Today, we did some problem-solving with an activity I found on MathPickle.com: Addition Boomerang. (Watch the video – it explains how the boomerangs work. Definitely worth the 5 minutes.)
I started with all 4 of the kids together and demonstrated how the boomerangs work. We started with one boomerang with a +1 to reach the target of 10. Then we changed it to +2 to the target of 10. The boys were seeing this as an easy activity, and liked the idea of going around the boomerang circle.
Next, I changed it to two boomerangs: +3 and +4 with the same target of 10. I asked them to find every combination, both successful and “fails.”
This is what we produced together:
After we discussed other combinations, they determined that they had found all the successful combinations. Anything else we we might try would result in similar fails. This discussion was incredible, because some of them still don’t always remember the commutative property of addition. We often have to review that if 3+4=7, then 4+3 also equals 7. Epiphany moment!
After our discussion, I paired them up and gave them their own boomerangs to solve. One group had to get to the target of 20 with +4 and +5. The other group needed to get to 12 with +2 and +3.
Here’s the beauty of what I witnessed today. One of my boys who is very fluent in addition facts well past 10 struggled with this activity at first. He didn’t understand what we were trying to do. After working with his partner, he exclaimed, “Oh! I get it!” Exuberant smiles followed. Those facts he memorized are beginning to come to life for him.
Another one of my boys who is not fluent in addition facts to 10 whizzed through this activity. He was counting so quickly, his partner had to ask him to slow down so he could figure it out as well. I can still ask him, “what is 4+5?” and it will take him as long as it takes to put up 4 fingers followed by 5 fingers. But when I asked him which combinations would work in his boomerang, he amazed me at how quickly he could come up with different combinations, AS WELL AS explain WHY. This is a kid who would fail a standardized fill-in-the-blank or multiple choice math test on addition facts to 10. Give him a method in which to find a pattern or solve a puzzle, and he is able to show exactly what he understands.
When parents have come to me over the years with concerns- or outright nervousness- about where their kids are in math, I have tried to reassure them that a) kids don’t learn at the same pace, b) knowing facts is NOT understanding mathematics, and c) kids need a variety of activities that help them explore the relationship of numbers in meaningful and relevant ways.
Drilling facts, and even emphasizing facts over understanding of the concrete and representational aspects of what numbers and operators mean does a lot of damage to how kids view “math.”
So here’s my advice:
- Take a deep breath. Your child’s math progress does not reflect poorly on you as a parent. I promise.
- If you have taken your child to a math tutoring business*, remember that it is a business. They will find something (anything!) wrong with your child’s progress to sell you their services.
- If you really want to help your child understand the relationship of numbers, find activities that involve, but do not focus on math. Baking, building, measuring, counting, budgeting for groceries– all of these are great ways to involve your child in something that requires some skills and concepts without it being the only focus. Math facts, by themselves, can be tedious and tiresome for a lot of kids (especially for those who have been told they are “behind”).
- One of my students can count by 7s because he is a huge football fan. Ask him how many points have been scored with 6 touchdowns… he knows the answer. And he is SIX. Football matters to him, so groups of 7s and 3s are meaningful to him, too. What matters to your child? Build on that.
- Puzzles and patterns are fabulous ways to help kids make sense of numbers. If your child loves patterns, but hates “math,” there is a disconnect here. Find puzzles that your child might enjoy and do them together. Be patient, and don’t feed answers.
- Do a little research on Concrete-Representational-Abstract instruction (CRA). This has been my underlying philosophy of how I help kids learn concepts in math (and music, for that matter), and I’ve seen kids’ understanding improve significantly. This method connects the HOW with the WHY.
- If you’re teaching math, where is your emphasis? I know many of you have pacing guides, material/textbooks to cover, and even scripts you are required to follow… but are you helping your students understand? If yes, please add some of your resources or suggestions in the comments. (Thanks!)
I’m fortunate to teach at a school** where we MAKE time for kids to explore and have those epiphany moments, whether it’s in their mathematic abilities, reading, asking questions, creating, building, or discovering their passions. (It’s a pretty awesome place to be a kid AND an adult who gets to witness it all.)
Above all else, I want to do what’s right for each of the children in my care every day. There’s a reason “Drill and Kill” became a thing in describing math practice activities. I don’t have any place for that when I want to help children understand.
(+10,000 points to you if you read all the way to the end. TL:DR is not in my vocabulary.)
*”math tutoring business” in this sense refers to corporate and for-profit businesses, not individuals.
**Shameless plug: if you want to witness in person what we do in our school, please join us at 5sigmaeducon.com next month!